Applying a genetic algorithm to the traveling salesman problem
 To understand what the traveling salesman problem (TSP) is, and why it's so problematic, let's briefly go over a classic example of the problem.
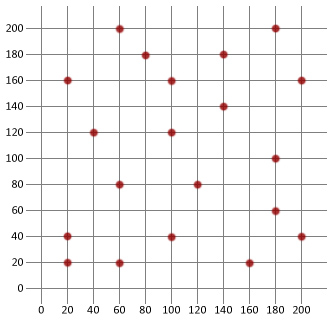
To understand what the traveling salesman problem (TSP) is, and why it's so problematic, let's briefly go over a classic example of the problem.Imagine you're a salesman and you've been given a map like the one opposite. On it you see that the map contains a total of 20 locations and you're told it’s your job to visit each of these locations to make a sell.
Before you set off on your journey you'll probably want to plan a route so you can minimize your travel time. Fortunately, humans are pretty good at this, we can easily work out a reasonably good route without needing to do much more than glance at the map. However, when we’ve found a route that we believe is optimal, how can we test if it's really the optimal route?
Well, in short, we can’t - at least not practically.
To understand why it's so difficult to prove the optimal route let’s consider a similar map with just 3 locations instead of the original 20. To find a single route, we first have to choose a starting location from the three possible locations on the map. Next, we’d have a choice of 2 cities for the second location, then finally there is just 1 city left to pick to complete our route. This would mean there are 3 x 2 x 1 different routes to pick in total.
That means, for this example, there are only 6 different routes to pick from. So for this case of just 3 locations it's reasonably trivial to calculate each of those 6 routes and find the shortest. If you're good at maths you may have already realized what the problem is here. The number of possible routes is a factorial of the number of locations to visit, and trouble with factorials is that they grow in size remarkably quick!
For example, the factorial of 10 is 3628800, but the factorial of 20 is a gigantic, 2432902008176640000.
So going back to our original problem, if we want to find the shortest route for our map of 20 locations we would have to evaluate 2432902008176640000 different routes! Even with modern computing power this is terribly impractical, and for even bigger problems, it’s close to impossible.
Finding a solution
Although it may not be practical to find the best solution for a problem like ours, we do have algorithms that let us discover close to optimum solutions such as the nearest neighbor algorithm and swarm optimization. These algorithms are capable of finding a ‘good-enough’ solution to the travelling salesman problem surprisingly quickly. In this tutorial however, we will be using genetic algorithms as our optimization technique.If you’re not already familiar with genetic algorithms and like to know how they work, then please have a look at the introductory tutorial below:
Creating a genetic algorithm for beginners
Finding a solution to the travelling salesman problem requires we set up a genetic algorithm in a specialized way. For instance, a valid solution would need to represent a route where every location is included at least once and only once. If a route contain a single location more than once, or missed a location out completely it wouldn't be valid and we would be valuable computation time calculating it's distance.
To ensure the genetic algorithm does indeed meet this requirement special types of mutation and crossover methods are needed.
Firstly, the mutation method should only be capable of shuffling the route, it shouldn't ever add or remove a location from the route, otherwise it would risk creating an invalid solution. One type of mutation method we could use is swap mutation.
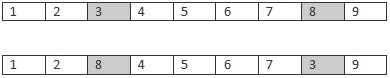
With swap mutation two location in the route are selected at random then their positions are simply swapped. For example, if we apply swap mutation to the following list, [1,2,3,4,5] we might end up with, [1,2,5,4,3]. Here, positions 3 and 5 were switched creating a new list with exactly the same values, just a different order. Because swap mutation is only swapping pre-existing values, it will never create a list which has missing or duplicate values when compared to the original, and that's exactly what we want for the traveling salesman problem.
Now we’ve dealt with the mutation method we need to pick a crossover method which can enforce the same constraint.
One crossover method that's able to produce a valid route is ordered crossover. In this crossover method we select a subset from the first parent, and then add that subset to the offspring. Any missing values are then adding to the offspring from the second parent in order that they are found.
To make this explanation a little clearer consider the following example:
Parents
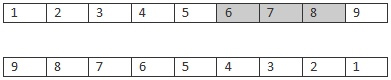
Offspring
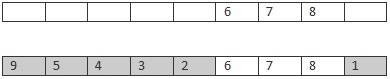
Here a subset of the route is taken from the first parent (6,7,8) and added to the offspring's route. Next, the missing route locations are adding in order from the second parent. The first location in the second parent's route is 9 which isn't in the offspring's route so it's added in the first available position. The next position in the parents route is 8 which is in the offspring's route so it's skipped. This process continues until the offspring has no remaining empty values. If implemented correctly the end result should be a route which contains all of the positions it's parents did with no positions missing or duplicated.
Creating the Genetic Algorithm
In literature of the traveling salesman problem since locations are typically refereed to as cities, and routes are refereed to as tours, we will adopt the standard naming conventions in our code.To start, let’s create a class that can encode the cities.
City.java
/*
* City.java
* Models a city
*/
package tsp;
public class City {
int x;
int y;
// Constructs a randomly placed city
public City(){
this.x = (int)(Math.random()*200);
this.y = (int)(Math.random()*200);
}
// Constructs a city at chosen x, y location
public City(int x, int y){
this.x = x;
this.y = y;
}
// Gets city's x coordinate
public int getX(){
return this.x;
}
// Gets city's y coordinate
public int getY(){
return this.y;
}
// Gets the distance to given city
public double distanceTo(City city){
int xDistance = Math.abs(getX() - city.getX());
int yDistance = Math.abs(getY() - city.getY());
double distance = Math.sqrt( (xDistance*xDistance) + (yDistance*yDistance) );
return distance;
}
@Override
public String toString(){
return getX()+", "+getY();
}
}
* City.java
* Models a city
*/
package tsp;
public class City {
int x;
int y;
// Constructs a randomly placed city
public City(){
this.x = (int)(Math.random()*200);
this.y = (int)(Math.random()*200);
}
// Constructs a city at chosen x, y location
public City(int x, int y){
this.x = x;
this.y = y;
}
// Gets city's x coordinate
public int getX(){
return this.x;
}
// Gets city's y coordinate
public int getY(){
return this.y;
}
// Gets the distance to given city
public double distanceTo(City city){
int xDistance = Math.abs(getX() - city.getX());
int yDistance = Math.abs(getY() - city.getY());
double distance = Math.sqrt( (xDistance*xDistance) + (yDistance*yDistance) );
return distance;
}
@Override
public String toString(){
return getX()+", "+getY();
}
}
Now we can create a class that holds all of our destination cities for our tour
TourManager.java
/*
* TourManager.java
* Holds the cities of a tour
*/
package tsp;
import java.util.ArrayList;
public class TourManager {
// Holds our cities
private static ArrayList destinationCities = new ArrayList<City>();
// Adds a destination city
public static void addCity(City city) {
destinationCities.add(city);
}
// Get a city
public static City getCity(int index){
return (City)destinationCities.get(index);
}
// Get the number of destination cities
public static int numberOfCities(){
return destinationCities.size();
}
}
* TourManager.java
* Holds the cities of a tour
*/
package tsp;
import java.util.ArrayList;
public class TourManager {
// Holds our cities
private static ArrayList destinationCities = new ArrayList<City>();
// Adds a destination city
public static void addCity(City city) {
destinationCities.add(city);
}
// Get a city
public static City getCity(int index){
return (City)destinationCities.get(index);
}
// Get the number of destination cities
public static int numberOfCities(){
return destinationCities.size();
}
}
Next we need a class that can encode our routes, these are generally referred to as tours so we'll stick to the convention.
Tour.java
/*
* Tour.java
* Stores a candidate tour
*/
package tsp;
import java.util.ArrayList;
import java.util.Collections;
public class Tour{
// Holds our tour of cities
private ArrayList tour = new ArrayList<City>();
// Cache
private double fitness = 0;
private int distance = 0;
// Constructs a blank tour
public Tour(){
for (int i = 0; i < TourManager.numberOfCities(); i++) {
tour.add(null);
}
}
public Tour(ArrayList tour){
this.tour = tour;
}
// Creates a random individual
public void generateIndividual() {
// Loop through all our destination cities and add them to our tour
for (int cityIndex = 0; cityIndex < TourManager.numberOfCities(); cityIndex++) {
setCity(cityIndex, TourManager.getCity(cityIndex));
}
// Randomly reorder the tour
Collections.shuffle(tour);
}
// Gets a city from the tour
public City getCity(int tourPosition) {
return (City)tour.get(tourPosition);
}
// Sets a city in a certain position within a tour
public void setCity(int tourPosition, City city) {
tour.set(tourPosition, city);
// If the tours been altered we need to reset the fitness and distance
fitness = 0;
distance = 0;
}
// Gets the tours fitness
public double getFitness() {
if (fitness == 0) {
fitness = 1/(double)getDistance();
}
return fitness;
}
// Gets the total distance of the tour
public int getDistance(){
if (distance == 0) {
int tourDistance = 0;
// Loop through our tour's cities
for (int cityIndex=0; cityIndex < tourSize(); cityIndex++) {
// Get city we're travelling from
City fromCity = getCity(cityIndex);
// City we're travelling to
City destinationCity;
// Check we're not on our tour's last city, if we are set our
// tour's final destination city to our starting city
if(cityIndex+1 < tourSize()){
destinationCity = getCity(cityIndex+1);
}
else{
destinationCity = getCity(0);
}
// Get the distance between the two cities
tourDistance += fromCity.distanceTo(destinationCity);
}
distance = tourDistance;
}
return distance;
}
// Get number of cities on our tour
public int tourSize() {
return tour.size();
}
// Check if the tour contains a city
public boolean containsCity(City city){
return tour.contains(city);
}
@Override
public String toString() {
String geneString = "|";
for (int i = 0; i < tourSize(); i++) {
geneString += getCity(i)+"|";
}
return geneString;
}
}
* Tour.java
* Stores a candidate tour
*/
package tsp;
import java.util.ArrayList;
import java.util.Collections;
public class Tour{
// Holds our tour of cities
private ArrayList tour = new ArrayList<City>();
// Cache
private double fitness = 0;
private int distance = 0;
// Constructs a blank tour
public Tour(){
for (int i = 0; i < TourManager.numberOfCities(); i++) {
tour.add(null);
}
}
public Tour(ArrayList tour){
this.tour = tour;
}
// Creates a random individual
public void generateIndividual() {
// Loop through all our destination cities and add them to our tour
for (int cityIndex = 0; cityIndex < TourManager.numberOfCities(); cityIndex++) {
setCity(cityIndex, TourManager.getCity(cityIndex));
}
// Randomly reorder the tour
Collections.shuffle(tour);
}
// Gets a city from the tour
public City getCity(int tourPosition) {
return (City)tour.get(tourPosition);
}
// Sets a city in a certain position within a tour
public void setCity(int tourPosition, City city) {
tour.set(tourPosition, city);
// If the tours been altered we need to reset the fitness and distance
fitness = 0;
distance = 0;
}
// Gets the tours fitness
public double getFitness() {
if (fitness == 0) {
fitness = 1/(double)getDistance();
}
return fitness;
}
// Gets the total distance of the tour
public int getDistance(){
if (distance == 0) {
int tourDistance = 0;
// Loop through our tour's cities
for (int cityIndex=0; cityIndex < tourSize(); cityIndex++) {
// Get city we're travelling from
City fromCity = getCity(cityIndex);
// City we're travelling to
City destinationCity;
// Check we're not on our tour's last city, if we are set our
// tour's final destination city to our starting city
if(cityIndex+1 < tourSize()){
destinationCity = getCity(cityIndex+1);
}
else{
destinationCity = getCity(0);
}
// Get the distance between the two cities
tourDistance += fromCity.distanceTo(destinationCity);
}
distance = tourDistance;
}
return distance;
}
// Get number of cities on our tour
public int tourSize() {
return tour.size();
}
// Check if the tour contains a city
public boolean containsCity(City city){
return tour.contains(city);
}
@Override
public String toString() {
String geneString = "|";
for (int i = 0; i < tourSize(); i++) {
geneString += getCity(i)+"|";
}
return geneString;
}
}
We also need to create a class that can hold a population of candidate tours
Population.java
/*
* Population.java
* Manages a population of candidate tours
*/
package tsp;
public class Population {
// Holds population of tours
Tour[] tours;
// Construct a population
public Population(int populationSize, boolean initialise) {
tours = new Tour[populationSize];
// If we need to initialise a population of tours do so
if (initialise) {
// Loop and create individuals
for (int i = 0; i < populationSize(); i++) {
Tour newTour = new Tour();
newTour.generateIndividual();
saveTour(i, newTour);
}
}
}
// Saves a tour
public void saveTour(int index, Tour tour) {
tours[index] = tour;
}
// Gets a tour from population
public Tour getTour(int index) {
return tours[index];
}
// Gets the best tour in the population
public Tour getFittest() {
Tour fittest = tours[0];
// Loop through individuals to find fittest
for (int i = 1; i < populationSize(); i++) {
if (fittest.getFitness() <= getTour(i).getFitness()) {
fittest = getTour(i);
}
}
return fittest;
}
// Gets population size
public int populationSize() {
return tours.length;
}
}
* Population.java
* Manages a population of candidate tours
*/
package tsp;
public class Population {
// Holds population of tours
Tour[] tours;
// Construct a population
public Population(int populationSize, boolean initialise) {
tours = new Tour[populationSize];
// If we need to initialise a population of tours do so
if (initialise) {
// Loop and create individuals
for (int i = 0; i < populationSize(); i++) {
Tour newTour = new Tour();
newTour.generateIndividual();
saveTour(i, newTour);
}
}
}
// Saves a tour
public void saveTour(int index, Tour tour) {
tours[index] = tour;
}
// Gets a tour from population
public Tour getTour(int index) {
return tours[index];
}
// Gets the best tour in the population
public Tour getFittest() {
Tour fittest = tours[0];
// Loop through individuals to find fittest
for (int i = 1; i < populationSize(); i++) {
if (fittest.getFitness() <= getTour(i).getFitness()) {
fittest = getTour(i);
}
}
return fittest;
}
// Gets population size
public int populationSize() {
return tours.length;
}
}
Next, the let's create a GA class which will handle the working of the genetic algorithm and evolve our population of solutions.
GA.java
/*
* GA.java
* Manages algorithms for evolving population
*/
package tsp;
public class GA {
/* GA parameters */
private static final double mutationRate = 0.015;
private static final int tournamentSize = 5;
private static final boolean elitism = true;
// Evolves a population over one generation
public static Population evolvePopulation(Population pop) {
Population newPopulation = new Population(pop.populationSize(), false);
// Keep our best individual if elitism is enabled
int elitismOffset = 0;
if (elitism) {
newPopulation.saveTour(0, pop.getFittest());
elitismOffset = 1;
}
// Crossover population
// Loop over the new population's size and create individuals from
// Current population
for (int i = elitismOffset; i < newPopulation.populationSize(); i++) {
// Select parents
Tour parent1 = tournamentSelection(pop);
Tour parent2 = tournamentSelection(pop);
// Crossover parents
Tour child = crossover(parent1, parent2);
// Add child to new population
newPopulation.saveTour(i, child);
}
// Mutate the new population a bit to add some new genetic material
for (int i = elitismOffset; i < newPopulation.populationSize(); i++) {
mutate(newPopulation.getTour(i));
}
return newPopulation;
}
// Applies crossover to a set of parents and creates offspring
public static Tour crossover(Tour parent1, Tour parent2) {
// Create new child tour
Tour child = new Tour();
// Get start and end sub tour positions for parent1's tour
int startPos = (int) (Math.random() * parent1.tourSize());
int endPos = (int) (Math.random() * parent1.tourSize());
// Loop and add the sub tour from parent1 to our child
for (int i = 0; i < child.tourSize(); i++) {
// If our start position is less than the end position
if (startPos < endPos && i > startPos && i < endPos) {
child.setCity(i, parent1.getCity(i));
} // If our start position is larger
else if (startPos > endPos) {
if (!(i < startPos && i > endPos)) {
child.setCity(i, parent1.getCity(i));
}
}
}
// Loop through parent2's city tour
for (int i = 0; i < parent2.tourSize(); i++) {
// If child doesn't have the city add it
if (!child.containsCity(parent2.getCity(i))) {
// Loop to find a spare position in the child's tour
for (int ii = 0; ii < child.tourSize(); ii++) {
// Spare position found, add city
if (child.getCity(ii) == null) {
child.setCity(ii, parent2.getCity(i));
break;
}
}
}
}
return child;
}
// Mutate a tour using swap mutation
private static void mutate(Tour tour) {
// Loop through tour cities
for(int tourPos1=0; tourPos1 < tour.tourSize(); tourPos1++){
// Apply mutation rate
if(Math.random() < mutationRate){
// Get a second random position in the tour
int tourPos2 = (int) (tour.tourSize() * Math.random());
// Get the cities at target position in tour
City city1 = tour.getCity(tourPos1);
City city2 = tour.getCity(tourPos2);
// Swap them around
tour.setCity(tourPos2, city1);
tour.setCity(tourPos1, city2);
}
}
}
// Selects candidate tour for crossover
private static Tour tournamentSelection(Population pop) {
// Create a tournament population
Population tournament = new Population(tournamentSize, false);
// For each place in the tournament get a random candidate tour and
// add it
for (int i = 0; i < tournamentSize; i++) {
int randomId = (int) (Math.random() * pop.populationSize());
tournament.saveTour(i, pop.getTour(randomId));
}
// Get the fittest tour
Tour fittest = tournament.getFittest();
return fittest;
}
}
* GA.java
* Manages algorithms for evolving population
*/
package tsp;
public class GA {
/* GA parameters */
private static final double mutationRate = 0.015;
private static final int tournamentSize = 5;
private static final boolean elitism = true;
// Evolves a population over one generation
public static Population evolvePopulation(Population pop) {
Population newPopulation = new Population(pop.populationSize(), false);
// Keep our best individual if elitism is enabled
int elitismOffset = 0;
if (elitism) {
newPopulation.saveTour(0, pop.getFittest());
elitismOffset = 1;
}
// Crossover population
// Loop over the new population's size and create individuals from
// Current population
for (int i = elitismOffset; i < newPopulation.populationSize(); i++) {
// Select parents
Tour parent1 = tournamentSelection(pop);
Tour parent2 = tournamentSelection(pop);
// Crossover parents
Tour child = crossover(parent1, parent2);
// Add child to new population
newPopulation.saveTour(i, child);
}
// Mutate the new population a bit to add some new genetic material
for (int i = elitismOffset; i < newPopulation.populationSize(); i++) {
mutate(newPopulation.getTour(i));
}
return newPopulation;
}
// Applies crossover to a set of parents and creates offspring
public static Tour crossover(Tour parent1, Tour parent2) {
// Create new child tour
Tour child = new Tour();
// Get start and end sub tour positions for parent1's tour
int startPos = (int) (Math.random() * parent1.tourSize());
int endPos = (int) (Math.random() * parent1.tourSize());
// Loop and add the sub tour from parent1 to our child
for (int i = 0; i < child.tourSize(); i++) {
// If our start position is less than the end position
if (startPos < endPos && i > startPos && i < endPos) {
child.setCity(i, parent1.getCity(i));
} // If our start position is larger
else if (startPos > endPos) {
if (!(i < startPos && i > endPos)) {
child.setCity(i, parent1.getCity(i));
}
}
}
// Loop through parent2's city tour
for (int i = 0; i < parent2.tourSize(); i++) {
// If child doesn't have the city add it
if (!child.containsCity(parent2.getCity(i))) {
// Loop to find a spare position in the child's tour
for (int ii = 0; ii < child.tourSize(); ii++) {
// Spare position found, add city
if (child.getCity(ii) == null) {
child.setCity(ii, parent2.getCity(i));
break;
}
}
}
}
return child;
}
// Mutate a tour using swap mutation
private static void mutate(Tour tour) {
// Loop through tour cities
for(int tourPos1=0; tourPos1 < tour.tourSize(); tourPos1++){
// Apply mutation rate
if(Math.random() < mutationRate){
// Get a second random position in the tour
int tourPos2 = (int) (tour.tourSize() * Math.random());
// Get the cities at target position in tour
City city1 = tour.getCity(tourPos1);
City city2 = tour.getCity(tourPos2);
// Swap them around
tour.setCity(tourPos2, city1);
tour.setCity(tourPos1, city2);
}
}
}
// Selects candidate tour for crossover
private static Tour tournamentSelection(Population pop) {
// Create a tournament population
Population tournament = new Population(tournamentSize, false);
// For each place in the tournament get a random candidate tour and
// add it
for (int i = 0; i < tournamentSize; i++) {
int randomId = (int) (Math.random() * pop.populationSize());
tournament.saveTour(i, pop.getTour(randomId));
}
// Get the fittest tour
Tour fittest = tournament.getFittest();
return fittest;
}
}
Now we can create our main method, add our cities and evolve a route for our travelling salesman problem.
TSP_GA.java
/*
* TSP_GA.java
* Create a tour and evolve a solution
*/
package tsp;
public class TSP_GA {
public static void main(String[] args) {
// Create and add our cities
City city = new City(60, 200);
TourManager.addCity(city);
City city2 = new City(180, 200);
TourManager.addCity(city2);
City city3 = new City(80, 180);
TourManager.addCity(city3);
City city4 = new City(140, 180);
TourManager.addCity(city4);
City city5 = new City(20, 160);
TourManager.addCity(city5);
City city6 = new City(100, 160);
TourManager.addCity(city6);
City city7 = new City(200, 160);
TourManager.addCity(city7);
City city8 = new City(140, 140);
TourManager.addCity(city8);
City city9 = new City(40, 120);
TourManager.addCity(city9);
City city10 = new City(100, 120);
TourManager.addCity(city10);
City city11 = new City(180, 100);
TourManager.addCity(city11);
City city12 = new City(60, 80);
TourManager.addCity(city12);
City city13 = new City(120, 80);
TourManager.addCity(city13);
City city14 = new City(180, 60);
TourManager.addCity(city14);
City city15 = new City(20, 40);
TourManager.addCity(city15);
City city16 = new City(100, 40);
TourManager.addCity(city16);
City city17 = new City(200, 40);
TourManager.addCity(city17);
City city18 = new City(20, 20);
TourManager.addCity(city18);
City city19 = new City(60, 20);
TourManager.addCity(city19);
City city20 = new City(160, 20);
TourManager.addCity(city20);
// Initialize population
Population pop = new Population(50, true);
System.out.println("Initial distance: " + pop.getFittest().getDistance());
// Evolve population for 100 generations
pop = GA.evolvePopulation(pop);
for (int i = 0; i < 100; i++) {
pop = GA.evolvePopulation(pop);
}
// Print final results
System.out.println("Finished");
System.out.println("Final distance: " + pop.getFittest().getDistance());
System.out.println("Solution:");
System.out.println(pop.getFittest());
}
}
* TSP_GA.java
* Create a tour and evolve a solution
*/
package tsp;
public class TSP_GA {
public static void main(String[] args) {
// Create and add our cities
City city = new City(60, 200);
TourManager.addCity(city);
City city2 = new City(180, 200);
TourManager.addCity(city2);
City city3 = new City(80, 180);
TourManager.addCity(city3);
City city4 = new City(140, 180);
TourManager.addCity(city4);
City city5 = new City(20, 160);
TourManager.addCity(city5);
City city6 = new City(100, 160);
TourManager.addCity(city6);
City city7 = new City(200, 160);
TourManager.addCity(city7);
City city8 = new City(140, 140);
TourManager.addCity(city8);
City city9 = new City(40, 120);
TourManager.addCity(city9);
City city10 = new City(100, 120);
TourManager.addCity(city10);
City city11 = new City(180, 100);
TourManager.addCity(city11);
City city12 = new City(60, 80);
TourManager.addCity(city12);
City city13 = new City(120, 80);
TourManager.addCity(city13);
City city14 = new City(180, 60);
TourManager.addCity(city14);
City city15 = new City(20, 40);
TourManager.addCity(city15);
City city16 = new City(100, 40);
TourManager.addCity(city16);
City city17 = new City(200, 40);
TourManager.addCity(city17);
City city18 = new City(20, 20);
TourManager.addCity(city18);
City city19 = new City(60, 20);
TourManager.addCity(city19);
City city20 = new City(160, 20);
TourManager.addCity(city20);
// Initialize population
Population pop = new Population(50, true);
System.out.println("Initial distance: " + pop.getFittest().getDistance());
// Evolve population for 100 generations
pop = GA.evolvePopulation(pop);
for (int i = 0; i < 100; i++) {
pop = GA.evolvePopulation(pop);
}
// Print final results
System.out.println("Finished");
System.out.println("Final distance: " + pop.getFittest().getDistance());
System.out.println("Solution:");
System.out.println(pop.getFittest());
}
}
Output:
Initial distance: 1996
Finished
Final distance: 940
Solution:
|60, 200|20, 160|40, 120|60, 80|20, 40|20, 20|60, 20|100, 40|160, 20|200, 40|180, 60|120, 80|140, 140|180, 100|200, 160|180, 200|140, 180|100, 120|100, 160|80, 180|
Finished
Final distance: 940
Solution:
|60, 200|20, 160|40, 120|60, 80|20, 40|20, 20|60, 20|100, 40|160, 20|200, 40|180, 60|120, 80|140, 140|180, 100|200, 160|180, 200|140, 180|100, 120|100, 160|80, 180|
As you can see in just 100 generations we were able to find a route just over twice as good as our original and probably pretty close to optimum.
Final Results:
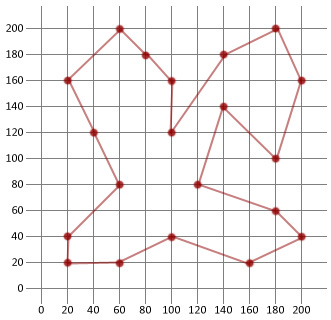
If you liked this tutorial you might also enjoy, Simulated Annealing for beginners
Author
 Hello, I'm Lee.
Hello, I'm Lee.I'm a developer from the UK who writes about technology and startups. Here you'll find articles and tutorials about things that interest me. If you want to hire me or know more about me head over to my about me page



