Creating a genetic algorithm for beginners
Introduction
A genetic algorithm (GA) is great for finding solutions to complex search problems. They're often used in fields such as engineering to create incredibly high quality products thanks to their ability to search a through a huge combination of parameters to find the best match. For example, they can search through different combinations of materials and designs to find the perfect combination of both which could result in a stronger, lighter and overall, better final product. They can also be used to design computer algorithms, to schedule tasks, and to solve other optimization problems. Genetic algorithms are based on the process of evolution by natural selection which has been observed in nature. They essentially replicate the way in which life uses evolution to find solutions to real world problems. Surprisingly although genetic algorithms can be used to find solutions to incredibly complicated problems, they are themselves pretty simple to use and understand.How they work
As we now know they're based on the process of natural selection, this means they take the fundamental properties of natural selection and apply them to whatever problem it is we're trying to solve.The basic process for a genetic algorithm is:
- Initialization - Create an initial population. This population is usually randomly generated and can be any desired size, from only a few individuals to thousands.
- Evaluation - Each member of the population is then evaluated and we calculate a 'fitness' for that individual. The fitness value is calculated by how well it fits with our desired requirements. These requirements could be simple, 'faster algorithms are better', or more complex, 'stronger materials are better but they shouldn't be too heavy'.
- Selection - We want to be constantly improving our populations overall fitness. Selection helps us to do this by discarding the bad designs and only keeping the best individuals in the population. There are a few different selection methods but the basic idea is the same, make it more likely that fitter individuals will be selected for our next generation.
- Crossover - During crossover we create new individuals by combining aspects of our selected individuals. We can think of this as mimicking how sex works in nature. The hope is that by combining certain traits from two or more individuals we will create an even 'fitter' offspring which will inherit the best traits from each of it's parents.
- Mutation - We need to add a little bit randomness into our populations' genetics otherwise every combination of solutions we can create would be in our initial population. Mutation typically works by making very small changes at random to an individuals genome.
- And repeat! - Now we have our next generation we can start again from step two until we reach a termination condition.
Termination
There are a few reasons why you would want to terminate your genetic algorithm from continuing it's search for a solution. The most likely reason is that your algorithm has found a solution which is good enough and meets a predefined minimum criteria. Offer reasons for terminating could be constraints such as time or money.Limitations
Imagine you were told to wear a blindfold then you were placed at the bottom of a hill with the instruction to find your way to the peak. You're only option is to set off climbing the hill until you notice you're no longer ascending anymore. At this point you might declare you've found the peak, but how would you know? In this situation because of your blindfolded you couldn't see if you're actually at the peak or just at the peak of smaller section of the hill. We call this a local optimum. Below is an example of how this local optimum might look: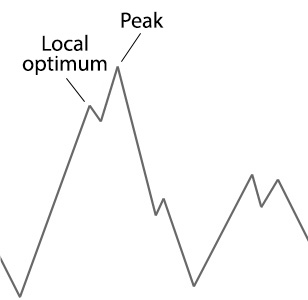
Unlike in our blindfolded hill climber, genetic algorithms can often escape from these local optimums if they are shallow enough. Although like our example we are often never able to guarantee that our genetic algorithm has found the global optimum solution to our problem. For more complex problems it is usually an unreasonable exception to find a global optimum, the best we can do is hope for is a close approximation of the optimal solution.
Implementing a basic binary genetic algorithm in Java
These examples are build in Java. If you don't have Java installed and you want to follow along please head over to the Java downloads page, http://www.oracle.com/technetwork/java/javase/downloads/index.htmlLet's take a look at the classes we're going to create for our GA:
- Population - Manages all individuals of a population
- Individual - Manages an individuals
- Algorithm - Manages our evolution algorithms such as crossover and mutation
- FitnessCalc - Allows us set a candidate solution and calculate an individual's fitness
Population.java
package simpleGa;
public class Population {
Individual[] individuals;
/*
* Constructors
*/
// Create a population
public Population(int populationSize, boolean initialise) {
individuals = new Individual[populationSize];
// Initialise population
if (initialise) {
// Loop and create individuals
for (int i = 0; i < size(); i++) {
Individual newIndividual = new Individual();
newIndividual.generateIndividual();
saveIndividual(i, newIndividual);
}
}
}
/* Getters */
public Individual getIndividual(int index) {
return individuals[index];
}
public Individual getFittest() {
Individual fittest = individuals[0];
// Loop through individuals to find fittest
for (int i = 0; i < size(); i++) {
if (fittest.getFitness() <= getIndividual(i).getFitness()) {
fittest = getIndividual(i);
}
}
return fittest;
}
/* Public methods */
// Get population size
public int size() {
return individuals.length;
}
// Save individual
public void saveIndividual(int index, Individual indiv) {
individuals[index] = indiv;
}
}
public class Population {
Individual[] individuals;
/*
* Constructors
*/
// Create a population
public Population(int populationSize, boolean initialise) {
individuals = new Individual[populationSize];
// Initialise population
if (initialise) {
// Loop and create individuals
for (int i = 0; i < size(); i++) {
Individual newIndividual = new Individual();
newIndividual.generateIndividual();
saveIndividual(i, newIndividual);
}
}
}
/* Getters */
public Individual getIndividual(int index) {
return individuals[index];
}
public Individual getFittest() {
Individual fittest = individuals[0];
// Loop through individuals to find fittest
for (int i = 0; i < size(); i++) {
if (fittest.getFitness() <= getIndividual(i).getFitness()) {
fittest = getIndividual(i);
}
}
return fittest;
}
/* Public methods */
// Get population size
public int size() {
return individuals.length;
}
// Save individual
public void saveIndividual(int index, Individual indiv) {
individuals[index] = indiv;
}
}
Individual.java
package simpleGa;
public class Individual {
static int defaultGeneLength = 64;
private byte[] genes = new byte[defaultGeneLength];
// Cache
private int fitness = 0;
// Create a random individual
public void generateIndividual() {
for (int i = 0; i < size(); i++) {
byte gene = (byte) Math.round(Math.random());
genes[i] = gene;
}
}
/* Getters and setters */
// Use this if you want to create individuals with different gene lengths
public static void setDefaultGeneLength(int length) {
defaultGeneLength = length;
}
public byte getGene(int index) {
return genes[index];
}
public void setGene(int index, byte value) {
genes[index] = value;
fitness = 0;
}
/* Public methods */
public int size() {
return genes.length;
}
public int getFitness() {
if (fitness == 0) {
fitness = FitnessCalc.getFitness(this);
}
return fitness;
}
@Override
public String toString() {
String geneString = "";
for (int i = 0; i < size(); i++) {
geneString += getGene(i);
}
return geneString;
}
}
public class Individual {
static int defaultGeneLength = 64;
private byte[] genes = new byte[defaultGeneLength];
// Cache
private int fitness = 0;
// Create a random individual
public void generateIndividual() {
for (int i = 0; i < size(); i++) {
byte gene = (byte) Math.round(Math.random());
genes[i] = gene;
}
}
/* Getters and setters */
// Use this if you want to create individuals with different gene lengths
public static void setDefaultGeneLength(int length) {
defaultGeneLength = length;
}
public byte getGene(int index) {
return genes[index];
}
public void setGene(int index, byte value) {
genes[index] = value;
fitness = 0;
}
/* Public methods */
public int size() {
return genes.length;
}
public int getFitness() {
if (fitness == 0) {
fitness = FitnessCalc.getFitness(this);
}
return fitness;
}
@Override
public String toString() {
String geneString = "";
for (int i = 0; i < size(); i++) {
geneString += getGene(i);
}
return geneString;
}
}
Algorithm.java
package simpleGa;
public class Algorithm {
/* GA parameters */
private static final double uniformRate = 0.5;
private static final double mutationRate = 0.015;
private static final int tournamentSize = 5;
private static final boolean elitism = true;
/* Public methods */
// Evolve a population
public static Population evolvePopulation(Population pop) {
Population newPopulation = new Population(pop.size(), false);
// Keep our best individual
if (elitism) {
newPopulation.saveIndividual(0, pop.getFittest());
}
// Crossover population
int elitismOffset;
if (elitism) {
elitismOffset = 1;
} else {
elitismOffset = 0;
}
// Loop over the population size and create new individuals with
// crossover
for (int i = elitismOffset; i < pop.size(); i++) {
Individual indiv1 = tournamentSelection(pop);
Individual indiv2 = tournamentSelection(pop);
Individual newIndiv = crossover(indiv1, indiv2);
newPopulation.saveIndividual(i, newIndiv);
}
// Mutate population
for (int i = elitismOffset; i < newPopulation.size(); i++) {
mutate(newPopulation.getIndividual(i));
}
return newPopulation;
}
// Crossover individuals
private static Individual crossover(Individual indiv1, Individual indiv2) {
Individual newSol = new Individual();
// Loop through genes
for (int i = 0; i < indiv1.size(); i++) {
// Crossover
if (Math.random() <= uniformRate) {
newSol.setGene(i, indiv1.getGene(i));
} else {
newSol.setGene(i, indiv2.getGene(i));
}
}
return newSol;
}
// Mutate an individual
private static void mutate(Individual indiv) {
// Loop through genes
for (int i = 0; i < indiv.size(); i++) {
if (Math.random() <= mutationRate) {
// Create random gene
byte gene = (byte) Math.round(Math.random());
indiv.setGene(i, gene);
}
}
}
// Select individuals for crossover
private static Individual tournamentSelection(Population pop) {
// Create a tournament population
Population tournament = new Population(tournamentSize, false);
// For each place in the tournament get a random individual
for (int i = 0; i < tournamentSize; i++) {
int randomId = (int) (Math.random() * pop.size());
tournament.saveIndividual(i, pop.getIndividual(randomId));
}
// Get the fittest
Individual fittest = tournament.getFittest();
return fittest;
}
}
public class Algorithm {
/* GA parameters */
private static final double uniformRate = 0.5;
private static final double mutationRate = 0.015;
private static final int tournamentSize = 5;
private static final boolean elitism = true;
/* Public methods */
// Evolve a population
public static Population evolvePopulation(Population pop) {
Population newPopulation = new Population(pop.size(), false);
// Keep our best individual
if (elitism) {
newPopulation.saveIndividual(0, pop.getFittest());
}
// Crossover population
int elitismOffset;
if (elitism) {
elitismOffset = 1;
} else {
elitismOffset = 0;
}
// Loop over the population size and create new individuals with
// crossover
for (int i = elitismOffset; i < pop.size(); i++) {
Individual indiv1 = tournamentSelection(pop);
Individual indiv2 = tournamentSelection(pop);
Individual newIndiv = crossover(indiv1, indiv2);
newPopulation.saveIndividual(i, newIndiv);
}
// Mutate population
for (int i = elitismOffset; i < newPopulation.size(); i++) {
mutate(newPopulation.getIndividual(i));
}
return newPopulation;
}
// Crossover individuals
private static Individual crossover(Individual indiv1, Individual indiv2) {
Individual newSol = new Individual();
// Loop through genes
for (int i = 0; i < indiv1.size(); i++) {
// Crossover
if (Math.random() <= uniformRate) {
newSol.setGene(i, indiv1.getGene(i));
} else {
newSol.setGene(i, indiv2.getGene(i));
}
}
return newSol;
}
// Mutate an individual
private static void mutate(Individual indiv) {
// Loop through genes
for (int i = 0; i < indiv.size(); i++) {
if (Math.random() <= mutationRate) {
// Create random gene
byte gene = (byte) Math.round(Math.random());
indiv.setGene(i, gene);
}
}
}
// Select individuals for crossover
private static Individual tournamentSelection(Population pop) {
// Create a tournament population
Population tournament = new Population(tournamentSize, false);
// For each place in the tournament get a random individual
for (int i = 0; i < tournamentSize; i++) {
int randomId = (int) (Math.random() * pop.size());
tournament.saveIndividual(i, pop.getIndividual(randomId));
}
// Get the fittest
Individual fittest = tournament.getFittest();
return fittest;
}
}
FitnessCalc.java
package simpleGa;
public class FitnessCalc {
static byte[] solution = new byte[64];
/* Public methods */
// Set a candidate solution as a byte array
public static void setSolution(byte[] newSolution) {
solution = newSolution;
}
// To make it easier we can use this method to set our candidate solution
// with string of 0s and 1s
static void setSolution(String newSolution) {
solution = new byte[newSolution.length()];
// Loop through each character of our string and save it in our byte
// array
for (int i = 0; i < newSolution.length(); i++) {
String character = newSolution.substring(i, i + 1);
if (character.contains("0") || character.contains("1")) {
solution[i] = Byte.parseByte(character);
} else {
solution[i] = 0;
}
}
}
// Calculate inidividuals fittness by comparing it to our candidate solution
static int getFitness(Individual individual) {
int fitness = 0;
// Loop through our individuals genes and compare them to our cadidates
for (int i = 0; i < individual.size() && i < solution.length; i++) {
if (individual.getGene(i) == solution[i]) {
fitness++;
}
}
return fitness;
}
// Get optimum fitness
static int getMaxFitness() {
int maxFitness = solution.length;
return maxFitness;
}
}
public class FitnessCalc {
static byte[] solution = new byte[64];
/* Public methods */
// Set a candidate solution as a byte array
public static void setSolution(byte[] newSolution) {
solution = newSolution;
}
// To make it easier we can use this method to set our candidate solution
// with string of 0s and 1s
static void setSolution(String newSolution) {
solution = new byte[newSolution.length()];
// Loop through each character of our string and save it in our byte
// array
for (int i = 0; i < newSolution.length(); i++) {
String character = newSolution.substring(i, i + 1);
if (character.contains("0") || character.contains("1")) {
solution[i] = Byte.parseByte(character);
} else {
solution[i] = 0;
}
}
}
// Calculate inidividuals fittness by comparing it to our candidate solution
static int getFitness(Individual individual) {
int fitness = 0;
// Loop through our individuals genes and compare them to our cadidates
for (int i = 0; i < individual.size() && i < solution.length; i++) {
if (individual.getGene(i) == solution[i]) {
fitness++;
}
}
return fitness;
}
// Get optimum fitness
static int getMaxFitness() {
int maxFitness = solution.length;
return maxFitness;
}
}
Now let's create our main class.
First we need to set a candidate solution (feel free to change this if you want to).
FitnessCalc.setSolution("1111000000000000000000000000000000000000000000000000000000001111");
Now we'll create our initial population, a population of 50 should be fine.
Population myPop = new Population(50,true);
Now we can evolve our population until we reach our optimum fitness
int generationCount = 0;
while(myPop.getFittest().getFitness() < FitnessCalc.getMaxFitness()){
generationCount++;
System.out.println("Generation: "+generationCount+" Fittest: "+myPop.getFittest().getFitness());
myPop = Algorithm.evolvePopulation(myPop);
}
System.out.println("Solution found!");
System.out.println("Generation: "+generationCount);
System.out.println("Genes:");
System.out.println(myPop.getFittest());
while(myPop.getFittest().getFitness() < FitnessCalc.getMaxFitness()){
generationCount++;
System.out.println("Generation: "+generationCount+" Fittest: "+myPop.getFittest().getFitness());
myPop = Algorithm.evolvePopulation(myPop);
}
System.out.println("Solution found!");
System.out.println("Generation: "+generationCount);
System.out.println("Genes:");
System.out.println(myPop.getFittest());
Here's the complete code for our main class:
GA.java
package simpleGa;
public class GA {
public static void main(String[] args) {
// Set a candidate solution
FitnessCalc.setSolution("1111000000000000000000000000000000000000000000000000000000001111");
// Create an initial population
Population myPop = new Population(50, true);
// Evolve our population until we reach an optimum solution
int generationCount = 0;
while (myPop.getFittest().getFitness() < FitnessCalc.getMaxFitness()) {
generationCount++;
System.out.println("Generation: " + generationCount + " Fittest: " + myPop.getFittest().getFitness());
myPop = Algorithm.evolvePopulation(myPop);
}
System.out.println("Solution found!");
System.out.println("Generation: " + generationCount);
System.out.println("Genes:");
System.out.println(myPop.getFittest());
}
}
public class GA {
public static void main(String[] args) {
// Set a candidate solution
FitnessCalc.setSolution("1111000000000000000000000000000000000000000000000000000000001111");
// Create an initial population
Population myPop = new Population(50, true);
// Evolve our population until we reach an optimum solution
int generationCount = 0;
while (myPop.getFittest().getFitness() < FitnessCalc.getMaxFitness()) {
generationCount++;
System.out.println("Generation: " + generationCount + " Fittest: " + myPop.getFittest().getFitness());
myPop = Algorithm.evolvePopulation(myPop);
}
System.out.println("Solution found!");
System.out.println("Generation: " + generationCount);
System.out.println("Genes:");
System.out.println(myPop.getFittest());
}
}
If everything's right, you should get an output similar to the following:
Generation: 1 Fittest: 40
Generation: 2 Fittest: 43
Generation: 3 Fittest: 50
Generation: 4 Fittest: 50
Generation: 5 Fittest: 52
Generation: 6 Fittest: 59
Generation: 7 Fittest: 59
Generation: 8 Fittest: 61
Generation: 9 Fittest: 61
Generation: 10 Fittest: 61
Generation: 11 Fittest: 63
Generation: 12 Fittest: 63
Generation: 13 Fittest: 63
Generation: 14 Fittest: 63
Generation: 15 Fittest: 63
Solution found!
Generation: 15
Genes:
1111000000000000000000000000000000000000000000000000000000001111
Generation: 2 Fittest: 43
Generation: 3 Fittest: 50
Generation: 4 Fittest: 50
Generation: 5 Fittest: 52
Generation: 6 Fittest: 59
Generation: 7 Fittest: 59
Generation: 8 Fittest: 61
Generation: 9 Fittest: 61
Generation: 10 Fittest: 61
Generation: 11 Fittest: 63
Generation: 12 Fittest: 63
Generation: 13 Fittest: 63
Generation: 14 Fittest: 63
Generation: 15 Fittest: 63
Solution found!
Generation: 15
Genes:
1111000000000000000000000000000000000000000000000000000000001111
Remember you're output isn't going to be exactly the same as above because of the inherent characteristics of a genetic algorithm.
And there you have it, that's a very basic binary GA. The great thing about a binary GA is that it is easy to represent any problem, although it might not always be the best way of going about it.
Want to apply a genetic algorithm to a real search problem? Check out the following tutorial, applying a genetic algorithm to the traveling salesman problem
Author
 Hello, I'm Lee.
Hello, I'm Lee.I'm a developer from the UK who writes about technology and startups. Here you'll find articles and tutorials about things that interest me. If you want to hire me or know more about me head over to my about me page



